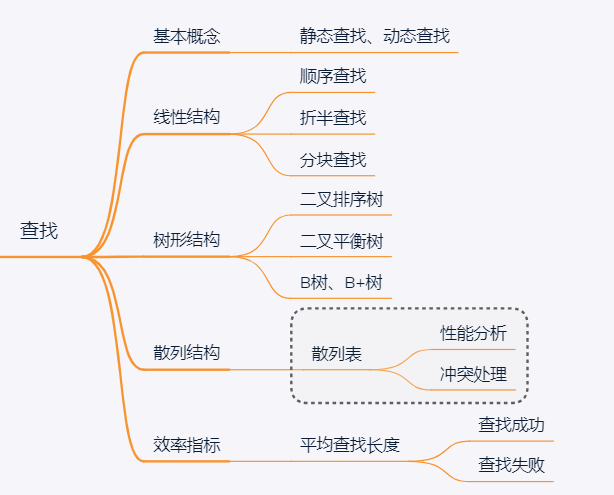
查找

基本概念

在数据集合中寻找满足某种条件的数据元素的过程称为查找

三个基本查找

顺序查找(线性查找)，主要用于在线性表中进行查找。从查找表的一端开始，顺序扫描查找表，依次将扫描到的关键字和待查找的值key进行比较。如果相等，则查找成功。如果扫描结束仍然没有发现相等的数据元素，则查找失败。
折半查找
折半查找仅适用于有序的顺序表
算法思路：
首先将给定值key与表中中间位置元素的关键字比较，若相等，则查找成功，返回该元素的存储位置；若不等，则所需查找的元素只能在中间元素以外的前半部分或后半部分中。然后在缩小的范围内继续进行同样的查找，如此重复直到找到为止，或者确定表中没有所需要查找的元素，则查找不成功，返回查找失败的信息。
分块查找
分块查找又称为索引顺序查找
需要额外建立一个索引表来存储索引，每个索引对应表中每一块。

二叉排序树

二叉排序树(Binary Search Tree 也叫二叉搜索树)或者是一棵空树，或者是具有以下性质的二叉树。
“左小右大”
①若左子树不空，则左子树上所有结点的值均小于它的根结点的值。
②若右子树不空，则右子树上所有结点的值均大于它的根结点的值。
③它的左右子树也是一棵二叉排序树。
对二叉排序树进行中序遍历可以得到一个递增的有序序列
由于二叉排序树的特点(左子树<根结点<右子树),所以每次查找一个关键字，需要先和根结点进行比较：
如果这个关键字小于根结点的值，则再到这个根结点的左子树进行同样的比较操作一直进行下去直到找到该关键字，表示查找成功，或者是空指针，表示查找失败。
如果这个关键字大于根结点的值，则再到这个根结点的右子树进行同样的比较操作一直进行下去直到找到该关键字，表示查找成功，或者是空指针，表示查找失败。
二叉排序树的目的，不是为了排序，而是为了提高查找和插入删除关键字的速度。

平衡二叉树

上一节我们讨论二叉排序树的性能的时候，发现不同形状的二叉排序树性能差异很大。主要反映在二叉树的相对高度上。
所以为了避免由于二叉排序树高度增长过快导致的性能降低，所以就需要对二叉排序树做出一定限制。
平衡二叉树(AVL树)是特殊的二叉排序树，特殊的地方在于左右子树的高度之差绝对值不超过1，而且左右子树又是一棵平衡二叉树。
定义结点左子树与右子树的高度差为该结点的平衡因子，则平衡二叉树结点的平衡因子的值只可能是−1、0或1。
平衡二叉树的建立过程和二叉排序树的建立过程是相似的，都是从一棵空树开始陆续插入结点。不同的地方在于对于平衡二叉树的建立过程中，由于插入结点可能会破坏结点的平衡性，所以需要进行平衡调整。
每插入一个结点，都要检查二叉排序树的平衡性，如果出现不平衡，那么平衡调整首先要找出最小不平衡子树，然后对这个最小不平衡子树进行调整。
LL调整(左孩子的左子树上插入结点导致)
RR调整(右孩子的右子树上插入结点导致)
LR调整(左孩子的右子树上插入结点导致)
RL调整(右孩子的左子树上插入结点导致)

B 树 和 B+ 树

2-3树是一种多路查找树：2和3的意思就是2-3树包含两种结点
2-3-4树也是一种多路查找树：2和3和4的意思就是2-3-4树包含三种结点
B树也是一种平衡的多路查找树，2-3树和2-3-4树都是B树的特例，我们把树中结点最大的孩子数目称为B树的阶。通常记为m。
一棵m阶B树或为空树，或为满足如下特性的m叉树：
1）树中每个结点至多有m棵子树。（即至多含有m-1个关键字) (“两棵子树指针夹着一个关键字”)
2）若根结点不是终端结点，则至少有两棵子树。(至少一个关键字)
3）除根结点外的所有非叶结点至少有 ⌈m/2⌉棵子树。（即至少含有⌈m/2⌉-1个关键字）
4）所有非叶结点的结构如下：
5）所有的叶子结点出现在同一层次上，不带信息。(就像是折半查找判断树中查找失败的结点)
B树是多路查找树，二叉排序树是二路查找，B树是多路查找，所以它是二叉排序树的拓展。因此，B树的查找操作和二叉排序树的查找操作非常类似。

B+树是常用于数据库和操作系统的文件系统中的一种用于查找的数据结构。
m阶的B+树与m阶的B树的主要差异在于：
1）在B+树中，具有n个关键字的结点只含有n棵子树，即每个关键字对应一棵子树；而在B树中，具有n个关键字的结点含有(n+1)棵子树。
2）在B+树中，每个结点（非根内部结点）关键字个数n的范围是 ⌈m/2⌉≤n≤m（根结点1≤n≤m），在B树中，每个结点（非根内部结点）关键字个数n的范围是⌈m/2⌉ -1≤n≤m-1（根结点：1≤n≤m-1）。
3）在B+树中，叶结点包含信息，所有非叶结点仅起到索引作用，非叶结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针，不含有该关键字对应记录的存储地址。
4）在B+树中，叶结点包含了全部关键字，即在非叶结点中出现的关键字也会出现在叶结点中；而在B树中，叶结点包含的关键字和其他结点包含的关键字是不重复的。

散列表 Hash

散列表：根据给定的关键字来计算出关键字在表中的地址的数据结构。也就是说，散列表建立了关键字和存储地址之间的一种直接映射关系。
散列函数：一个把查找表中的关键字映射成该关键字对应的地址的函数，记为 Hash(key) = Addr。
散列函数可能会把两个或两个以上的不同关键字映射到同一地址，称这种情况为“冲突”，这些发生碰撞的不同关键字称为同义词。