激活函数
为什么需要激活函数
从数学上看,神经网络是一个多层复合函数。激活函数在很早以前就被引入,其作用是保证神经网络的非线性,因为线性函数无论怎样复合结果还是线性的。
$$\hat y = X W_1 W_2 = X W_3$$
$$relu(x) = max(x,0)$$
为保证非线性,激活函数必须为非线性函数,但仅仅具有非线性是不够的。神经网络在本质上是一个复合函数,这会让我们思考一个问题:这个函数的建模能力有多强?即它能模拟什么样的目标函数?
已经证明,只要激活函数选择得当,神经元个数足够多,使用3层即包含一个隐含层的神经网络就可以实现对任何一个从输入向量到输出向量的连续映射函数的逼近,这个结论称为万能逼近(universal approximation)定理。
激活函数的主要作用是提供网络的非线性表达建模能力,想象一下如果没有激活函数,那么神经网络只能表达线性映射,此刻即便是有再多的隐藏层,其整个网络和单层的神经网络都是等价的。因此正式由于激活函数的存在,深度神经网络才具有了强大的非线性学习能力。
Loss Cost Object Function
损失函数(Loss Function )是定义在单个样本上的,算的是一个样本的误差。
代价函数(Cost Function )是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。
目标函数(Object Function)定义为:最终需要优化的函数。等于经验风险+结构风险(也就是Cost Function + 正则化项)。
关于目标函数和代价函数的区别还有一种通俗的区别:
目标函数是最大化或者最小化,而代价函数是最小化
反向传播(用于优化神网参数)
根据损失函数计算的误差通过反向传播的方式,指导深度网络参数的更新优化。通过定义损失函数,然后通过计算网络真实输出和真实标签之间的误差,得到网络的损失值:loss;
最后通过 loss.backward() 完成误差的反向传播,通过pytorch的内在机制完成自动求导得到每个参数的梯度。需要注意,在机器学习或者深度学习中,我们需要通过修改参数使得损失函数最小化或最大化,一般是通过梯度进行网络模型的参数更新,通过 loss 的计算和误差反向传播,我们得到网络中,每个参数的梯度值,后面我们再通过优化算法进行网络参数优化更新。在更新网络参数时,我们需要选择一种调整模型参数更新的策略,即优化算法。在pytorch中,torch.optim是一个实现各种优化算法的包,可以直接通过这个包进行调用。
Backpropagation, an abbreviation for “backward propagation of errors”, is a common method of training artificial neural networks used in conjunction with an optimization method such as gradient descent. The method calculates the gradient of a loss function with respect to all the weights in the network. The gradient is fed to the optimization method which in turn uses it to update the weights, in an attempt to minimize the loss function.
采取反向传播的原因:首先,深层网络由许多线性层和非线性层堆叠而来,每一层非线性层都可以视为是一个非线性函数(非线性来自于非线性激活函数),因此整个深度网络可以视为是一个复合的非线性多元函数。
我们最终的目的是希望这个非线性函数很好的完成输入到输出之间的映射,也就是找到让损失函数取得极小值。所以最终的问题就变成了一个寻找函数最小值的问题,在数学上,很自然的就会想到使用梯度下降来解决。
ReLU(Rectified Linear Units)
函数表达式:$f(x) = max(0,x)$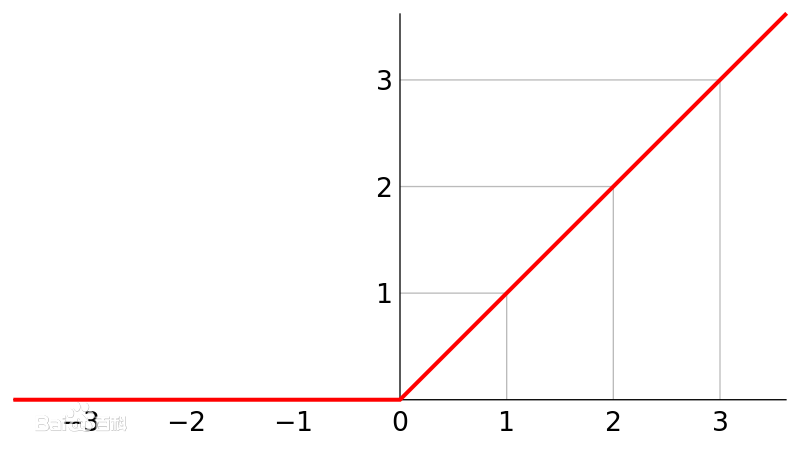
导数:当 x > 0 时,$f’(x) = 1$,当 x < 0 时,$f’(x) = 0$
优点:
当 x < 0 时,ReLU 硬饱和,而当 x > 0 时,则不存在饱和问题。
所以,ReLU 能够在 x > 0 时保持梯度不衰减,从而缓解梯度消失问题。这让我们能够直接以监督的方式训练深度神经网络,而无需依赖无监督的逐层预训练。
缺点:
随着训练的推进,部分输入会落入硬饱和区,导致对应权重无法更新。这种现象被称为“神经元死亡”。与 Sigmoid 类似,ReLU 的输出均值也大于 0,偏移现象和神经元死亡会共同影响网络的收敛性。
激活函数 softmax
softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类。
更形象的如下图: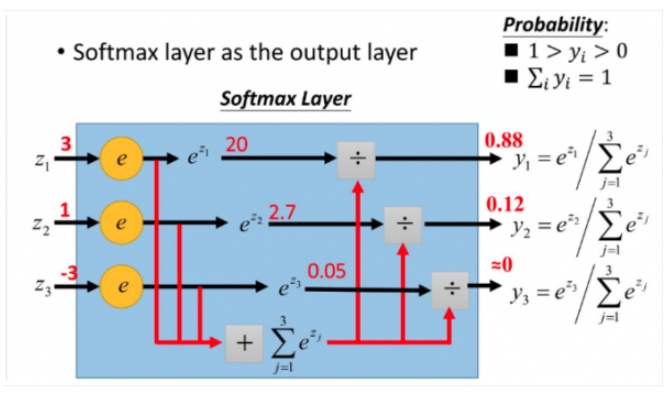
softmax 计算公式:$y_{i}=\frac{e^{z_{i}}}{\sum_{j}^{}{e^{z_{j}}}}$
在神经网络的计算当中,我们经常需要计算按照神经网络的正向传播计算的分数S1,和按照正确标注计算的分数S2,之间的差距,计算 Loss,才能应用反向传播。
当 Loss 定义为交叉熵, NLL:$L_{i} = -\log(\frac{e^{z_{i}}}{\sum_{j}e^{z_j}})$,
输出层我们一般选用softmax作为激活函数。
Why softmax?
- 计算求导上非常方便
- softmax函数值表示数据正确分类的值,它占的比重越大,这个样本的loss也就越小
softmax 回归分析 scratch version
from pathlib import Path
import requests
import pickle
import gzip
from matplotlib import pyplot
import numpy as np
import torchvision
import torch
torchvision.datasets.mnist
PATH = Path("...")
with gzip.open(PATH.as_posix(), "rb") as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding="latin-1")
pyplot.imshow(x_train[0].reshape((28, 28)), cmap="gray")
pyplot.show() # 显示图像
x_train, y_train, x_valid, y_valid = map(
torch.tensor, (x_train, y_train, x_valid, y_valid))
n, chhh = x_train.shape
x_train, x_train.shape, y_train.min(), y_train.max()
import math
weights = torch.randn(784, 10) / math.sqrt(784)
weights.requires_grad_()
bias = torch.zeros(10, requires_grad=True)
def log_softmax(x):
return x - x.exp().sum(-1).log().unsqueeze(-1)
def model(xb):
"""model
the @ stands for the dot product operation
:param xb: input
:return:
"""
return log_softmax(xb @ weights + bias)
bs = 64 # batch size
xb = x_train[0:bs] # a mini-batch from x
preds = model(xb) # predictions
def nll(input, target):
return -input[range(target.shape[0]), target].mean()
loss_func = nll
yb = y_train[0:bs]
def accuracy(out, yb):
preds = torch.argmax(out, dim=1)
return (preds == yb).float().mean()
print(accuracy(preds, yb))
from IPython.core.debugger import set_trace
lr = 0.5 # learning rate
epochs = 2 # how many epochs to train for
for epoch in range(epochs):
for i in range((n - 1) // bs + 1):
# set_trace()
if i==781:
print("")
start_i = i * bs
end_i = start_i + bs
xb = x_train[start_i:end_i]
yb = y_train[start_i:end_i]
pred = model(xb)
loss = loss_func(pred, yb)
loss.backward()
with torch.no_grad():
weights -= weights.grad * lr
bias -= bias.grad * lr
weights.grad.zero_()
bias.grad.zero_()
print(loss,accuracy(pred, yb))
print(loss_func(model(xb), yb), accuracy(model(xb), yb))
激活函数 sigmoid
Sigmoid 是一个可微的有界函数,在各点均有非负的导数。
当 x→∞ 时,S(x)→1;当 x→−∞ 时,S(x)→0。常用于二元分类(Binary Classification)问题,以及神经网络的激活函数(Activation Function)(把线性的输入转换为非线性的输出)
其实logistic函数也就是经常说的sigmoid函数,它的几何形状也就是一条sigmoid曲线(S型曲线)。其导数的小于等于 0.25
在二元分类的情况下,Softmax 退化为了 Sigmoid。
$$
\sigma(x) = \frac{1}{(1+e^{-x})}
$$
def sigmoid(x):
"""
sigmoid激活函数
:param x: 输入
:return: sigmoid(x)
"""
return 1/(1 + np.exp(-x))
梯度消失和梯度爆炸
反向传播算法计算误差项时每一层都要乘以本层激活函数的导数。如果激活函数导数的绝对值值小于1,多次连乘之后误差项很快会衰减到接近于0,参数的梯度值由误差项计算得到,从而导致前面层的权重梯度接近于0,参数没有得到有效更新,这称为 梯度 消失问题。
与之相反的是 梯度爆炸 问题,如果激活函数导数的绝对大于 1,多次乘积之后权重值会趋向于非常大的数,这称为梯度爆炸。
例如 Sigmoid 导数的取值范围在 0-0.25 之间,而我们初始化的网络权值通常都小于 1,因此,当层数增多时,小于 0 的值不断相乘,最后就导致梯度消失的情况出现。同理,梯度爆炸的问题也就很明显了,就是当权值$|w|$过大时,导致$|\sigma’(z)w| > 1$ ,最后大于 1 的值不断相乘,就会产生梯度爆炸。
- 解决神经网络中梯度消失问题的两种方法?
其实梯度爆炸和梯度消失问题都是因为网络太深,网络权值更新不稳定造成的,本质上是因为梯度反向传播中的连乘效应。对于更普遍的梯度消失问题,可以考虑用ReLU激活函数取代sigmoid激活函数。另外,LSTM的结构设计也可以改善RNN中的梯度消失问题。 - 解决梯度爆炸的方法?
梯度修剪,即当梯度的绝对值大于 M(M 是一个很大的数字)时,设梯度为 ±M。
为什么使用梯度下降来优化神经网络参数?
方向导数的本质是一个数值,简单来说其定义为: 一个函数沿指定方向的变化率。
$\frac{\partial f }{\partial l} = \frac{\partial f }{ \partial x} cos\alpha + \frac{\partial f}{\partial y} sin\alpha $
梯度与方向导数是有本质区别的,梯度其实是一个向量,其定义为:一个函数对于其自变量分别求偏导数,这些偏导数所组成的向量就是函数的梯度。
$grad f(x,y) = \frac{\partial f}{\partial x} i + \frac{\partial f}{\partial y} j$
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是解析解。
参考资料:
sigmoid函数图像: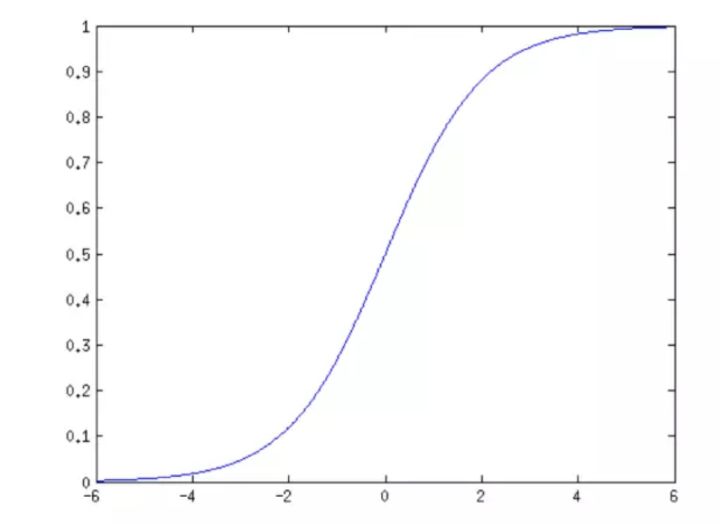
常用的激活函数以及相应的导数:
梯度下降:
https://www.jianshu.com/p/c7e642877b0e
方向导数与梯度的关系:
https://blog.csdn.net/weixin_40752830/article/details/90232461
http://netedu.xauat.edu.cn/jpkc/netedu/jpkc/gdsx/homepage/5jxsd/51/513/5308/530807.htm
Understanding the backward pass through Batch Normalization Layer
https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html
http://cs231n.github.io/optimization-2/#sigmoid
激活函数及选择经验
请多多指教。
文章标题:激活函数
本文作者:顺强
发布时间:2019-02-02, 23:59:00
原始链接:http://shunqiang.ml/cnn-activate-function/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

