Batch Normalization

论文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》
论文的着眼点：网络中各层的输入受到其前面各层参数的影响，当网络加深时网络参数的微小变动会被逐渐放大。让网络的各层输入保持同一分布有利于提升训练效率。作者提出Batch Normalization使网络各层的输入保持均值和方差稳定。

Look at the last line of the algorithm. After normalizing the input x the result is squashed through a linear function with parameters gamma and beta. These are learnable parameters of the BatchNorm Layer and make it basically possible to say “Hey!! I don’t want zero mean/unit variance input, give me back the raw input - it’s better for me.” If $gamma = sqrt(var(x))$ and $beta = mean(x)$, the original activation is restored. This is, what makes BatchNorm really powerful. We initialize the BatchNorm Parameters to transform the input to zero mean/unit variance distributions but during training they can learn that any other distribution might be better.
it’s called “Batch” Normalization because we perform this transformation and calculate the statistics only for a subpart (a batch) of the entire trainingsset.
Batch Normalization 主要作用：

1. 降低因为网络层输入的数据分布变动带来的网络参数剧烈变化，加速网络收敛。
2. 降低网络在反向计算过程中对大尺度参数变化的敏感性，使网络参数更新更加稳定。例如，网络训练过程中较大的学习率会带来大尺度的参数变化，进而再反向传播过程中造成model explosion，而加入Batch Normalization后，因为每层的输入都被范化，使得反向求导过程里参数的大尺度变化对参数更新的影响减小。

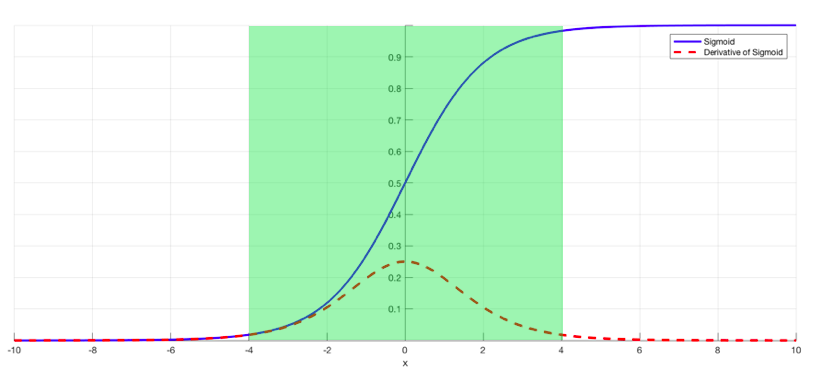
Finally, batch normalization layers can also resolve the issue. As stated before, the problem arises when a large input space is mapped to a small one, causing the derivatives to disappear. In Image 1, this is most clearly seen at when |x| is big. Batch normalization reduces this problem by simply normalizing the input so |x| doesn’t reach the outer edges of the sigmoid function. As seen in Image 3, it normalizes the input so that most of it falls in the green region, where the derivative isn’t too small.

def batchnorm_forward(x, gamma, beta, eps):
    """bn forward
    """
    N, D = x.shape
    #step1: calculate mean
    mu = 1./N * np.sum(x, axis = 0)
    #step2: subtract mean vector of every trainings example
    xmu = x - mu
    #step3: following the lower branch - calculation denominator
    sq = xmu ** 2
    #step4: calculate variance
    var = 1./N * np.sum(sq, axis = 0)
    #step5: add eps for numerical stability, then sqrt
    sqrtvar = np.sqrt(var + eps)
    #step6: invert sqrtwar
    ivar = 1./sqrtvar
    #step7: execute normalization
    xhat = xmu * ivar
    #step8: Nor the two transformation steps
    gammax = xhat * gamma
    #step9
    out = gammax + beta
    #store intermediate
    cache = (xhat,gamma,xmu,ivar,sqrtvar,var,eps)
    return out, cache

根据链式求导法则进行反向传递：
https://en.wikipedia.org/wiki/Chain_rule

def batchnorm_backward(dout, cache):
    #unfold the variables stored in cache
    xhat,gamma,xmu,ivar,sqrtvar,var,eps = cache
    #get the dimensions of the input/output
    N,D = dout.shape
    #step9
    dbeta = np.sum(dout, axis=0)
    dgammax = dout #not necessary, but more understandable
    #step8
    dgamma = np.sum(dgammax*xhat, axis=0)
    dxhat = dgammax * gamma
    #step7
    divar = np.sum(dxhat*xmu, axis=0)
    dxmu1 = dxhat * ivar
    #step6
    dsqrtvar = -1. /(sqrtvar**2) * divar
    #step5
    dvar = 0.5 * 1. /np.sqrt(var+eps) * dsqrtvar
    #step4
    dsq = 1. /N * np.ones((N,D)) * dvar
    #step3
    dxmu2 = 2 * xmu * dsq
    #step2
    dx1 = (dxmu1 + dxmu2)
    dmu = -1 * np.sum(dxmu1+dxmu2, axis=0)
    #step1
    dx2 = 1. /N * np.ones((N,D)) * dmu
    #step0
    dx = dx1 + dx2
    return dx, dgamma, dbeta

如果BN的期望和标准差是每个mini-batch各自计算得出的，那么batch_size不要设太小，以免每个mini-batch得到的期望和标准差波动太大。

为什么需要归一化呢？其一，因为机器学习的训练本质上是让模型学习到数据的分布。如果训练集的分布与测试集的分布有很大不同，那么训练出来的模型泛化能力就差，人们自然希望先把训练集和测试集分布调整到相近再训练；其二，实践表明，一个好的数据分布，有利于加速模型的训练及减少不收敛出现的概率，人们自然希望把数据调整到“好的分布”再训练。
数据预处理在机器学习领域还够用，但是到了深度学习领域，就显得力不从心了：因为深度网络很深，每一层过后，数据的分布都会产生一定的变化；浅层的微小变化经过一层层放大，到了深层就是很大的变化了。
论文把这样现象叫做“Internal Covariate Shift”。

NIPS 2018上的对BN作用解释的文章，推翻了之前BN能防止”internal covariate shift”现象的说法：
Batch normalization and internal covariate shift (ICS)

1. 论文认为BN与ICS不相关（增加了ICS，BN的作用依然很好），
2. 结果显示BN并不能减少ICS，相反，还会有一定程度上的增加，结论就是BN并不能减少ICS
   Why does BatchNorm work?
   论文认为BN的作用在于使得loss landscape更加光滑：

参考链接：
https://zhuanlan.zhihu.com/p/52132614
http://cs231n.github.io/optimization-2/#sigmoid
Understanding the backward pass through Batch Normalization Layer
https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html
https://zhuanlan.zhihu.com/p/38683831