二维卷积层

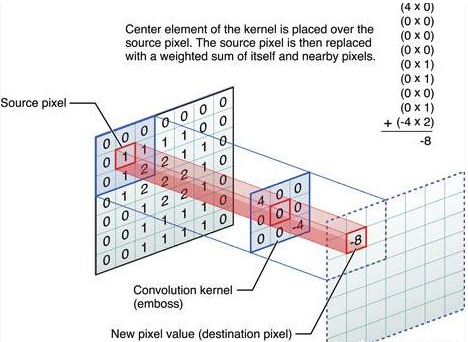
卷积神经网络（convolutional neural network）是含有卷积层（convolutional layer）的神经网络。本章中介绍的卷积神经网络均使用最常见的二维卷积层。它有高和宽两个空间维度，常用来处理图像数据。本节中，我们将介绍简单形式的二维卷积层的工作原理。

二维互相关运算

虽然卷积层得名于卷积（convolution）运算，但我们通常在卷积层中使用更加直观的互相关（cross-correlation）运算。在二维卷积层中，一个二维输入数组和一个二维核（kernel）数组通过互相关运算输出一个二维数组。
我们用一个具体例子来解释二维互相关运算的含义。如图5.1所示，输入是一个高和宽均为3的二维数组。我们将该数组的形状记为$3 \times 3$或（3，3）。核数组的高和宽分别为2。该数组在卷积计算中又称卷积核或过滤器（filter）。卷积核窗口（又称卷积窗口）的形状取决于卷积核的高和宽，即$2 \times 2$。图5.1中的阴影部分为第一个输出元素及其计算所使用的输入和核数组元素：$0\times0+1\times1+3\times2+4\times3=19$。

在二维互相关运算中，卷积窗口从输入数组的最左上方开始，按从左往右、从上往下的顺序，依次在输入数组上滑动。当卷积窗口滑动到某一位置时，窗口中的输入子数组与核数组按元素相乘并求和，得到输出数组中相应位置的元素。图5.1中的输出数组高和宽分别为2，其中的4个元素由二维互相关运算得出：

$$
0\times0+1\times1+3\times2+4\times3=19, \\
1\times0+2\times1+4\times2+5\times3=25, \\
3\times0+4\times1+6\times2+7\times3=37, \\
4\times0+5\times1+7\times2+8\times3=43.
$$

下面我们将上述过程实现在 corr2d 函数里。它接受输入数组 X 与核数组 K ，并输出数组 Y 。

Proof of Separable Convolution 2D

1 * 1 卷积

最初1x1卷积是在Network in Network中提出的，之后1x1convolution最初在GoogLeNet中大量使用，1x1卷积有以下几个特点：

• 用于降维或者升维，可以灵活控制特征图filter个数
• 减少参数量，特征图filter少了，参数量也会减少。
• 在卷积之后增加了非线性特征（添加激活函数）。
• 实现信息的通道整合和交互，以及具有升维/降维的能力。

卷积核是否越大越好？
这个要具体问题具体分析，在不同的领域大卷积核和小卷积核分别能取得不错的效果。并且在设置卷积核的时候一个常识是不能设得过大也不能过小，1 * 1 卷积只适合做分离卷积任务而不能对输入的原始特征做有效的特征抽取，而极大的卷积核通常会组合过多无用的特征浪费大量的计算资源。

转置卷积

转置卷积是先对原始特征矩阵进行填充使其维度扩大到目标输出维度，然后进行普通的卷积操作的过程，其输入到输出的维度变换关系恰好和普通的卷积变换关系相反，但这个变换并不是卷积真正的逆变换操作，我们通常将其称为转置卷积(Transpose Convolution)而不是反卷积(Deconvolution)。转置卷积常见于目标检测领域中对小目标的检测以及图像分割领域还原输入图像尺度如FCN中。如下图所示，其中下图数输入，上图是输出：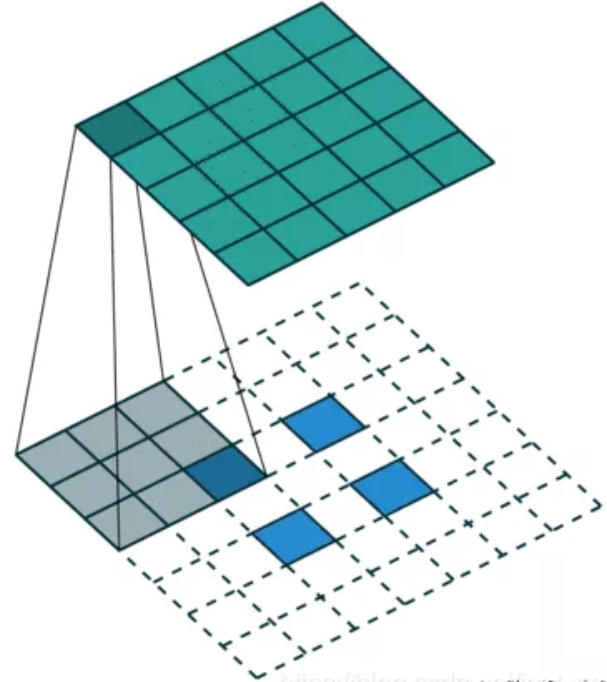

扩张卷积（带孔卷积或空洞卷积）Dilated Convolution(Atrous Convolution)

这是一种特殊的卷积，引入了一个称为扩展率(Dilation Rate)的参数，使得同样尺寸的卷积核可以获得更大的感受野，相应的在相同感受视野的前提下比普通卷积采用更少的参数。举个例子，同样是卷积核，扩张卷积可以获得范围的区域特征，在图像分割领域被广泛应用。如下图所示：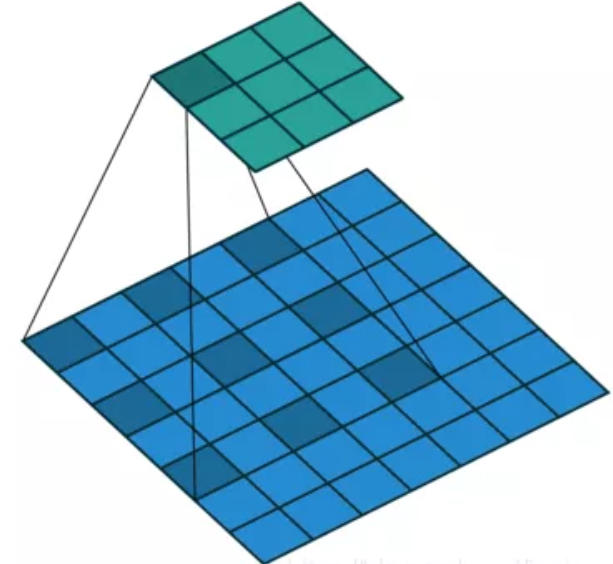

使用dilated convolution对大物体的效果会有一定效果，但是对小物体来说并不友好，小物体所需要的感受野并不需要太大。所以如何同时处理好不同大小物体之间的关系是使用空洞卷积的关键。

组卷积 Grouped Convolutions

组卷积最初是在AlexNet中提出的，之后被大量应用在ResNeXt网络结构中，提出的动机就是通过将feature 划分为不同的组来降低模型计算复杂度。
所谓分组就是将输入feature map的通道进行分组，然后每个组内部进行卷积操作，最终将得到的组卷积的结果Concate到一起，得到输出的feature map。
ResNeXt是ResNet和Inception的结合，其每个分支都采用的相同的拓扑结构。ResNeXt本质是使用组卷积（Grouped Convolutions），通过基数( cardinality )来控制组的数量。
使用组卷积的优点：

• 训练效率高。
  由于卷积被分为几个不同的组，每个组的计算就可以分配给不同的GPU核心来进行计算。这种结构的设计更符合GPU并行计算的要求，这也能解释为何ResNeXt在GPU上效率要高于Inception模块。
• 模型效率高。
  模型参数随着组数或者基数的增加而减少。
• 效果好。
  分组卷积可能能够比普通卷积组成的模型效果更优，这是因为滤波器之间的关系是稀疏的，而划分组以后对模型可以起到一定正则化的作用。从COCO数据集榜单就可以看出来，有很多是ResNeXt101作为backbone的模型在排行榜非常靠前的位置。
  A Tutorial on Filter Groups (Grouped Convolution)

可分离卷积 Separable Convolutions

可分离卷积可以分为空间可分离卷积(Spatially Separable Convolutions)和深度可分离卷积(depthwise separable convolution)。
假设 feature 的 size 为 [channel, height , width]
空间也就是指：[height, width]这两维度组成的。
深度也就是指：channel 这一维度。

空间可分离

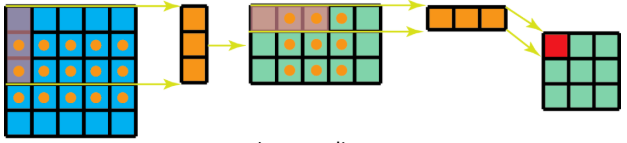
• 使用 3x1 的 filter，所需计算量为：15*3=45
• 使用 1x3 的 filter，所需计算量为：9*3=27
  总共需要 72 次乘法就可以得到最终结果，要小于普通卷积的 3*3*3 = 81 次乘法。
  注意：
• 虽然空间可分离卷积节省了计算成本，但是一般情况很少用到。原因是并非所有的 kernel 都可以分为两个较小的 kernel 。
• 空间可分离卷积可能会带来一定的信息损失；如果将全部的传统卷积替换为空间可分离卷积，将影响模型的容量, 这样得到的训练结果可能是次优的。

深度可分离卷积

这是在轻量级模型算法优化中经常会使用到的一种卷积方式，标准的卷积操作是对原始图像$HWC$三个方向的卷积运算，假设现在有 K 个相同尺寸卷积核，这样的操作计算量为$HWCK$个。若将长宽与深度方向的卷积操作分离出变为$HW$与$C$的两个卷积操作，则同样的卷积核数量 K ，现在的计算量变成了$(HW+C)K$个，也可以得到相同维度的输出。
主要有两个部分组成：

• Depthwise Convolution: 独立地施加在每个通道的空间卷积
• Pointwise Convolution: 1x1 convolution,通过深度卷积将通道输出投影到一个新的通道空间。
  深度可分离卷积在模型压缩和一些轻量级卷积神经网络中被广泛应用。
  Xception 与 MobileNet 的点滴

Flattened Convolutions

最初在 Flattened Convolutional Neural Networks for Feedforward Acceleration 中提出，是 2015 年 ICLR 的 workshop 。
Flattened Convolution 将标准的卷积核拆分成 3 个 1D 卷积核（空间可分离卷积只拆分HxW维度），可以极大地降低了计算成本。
Reason of usage same as 1x1 convs from NiN networks, but now not only features dimension set to 1, but also one of another dimensions: width or height.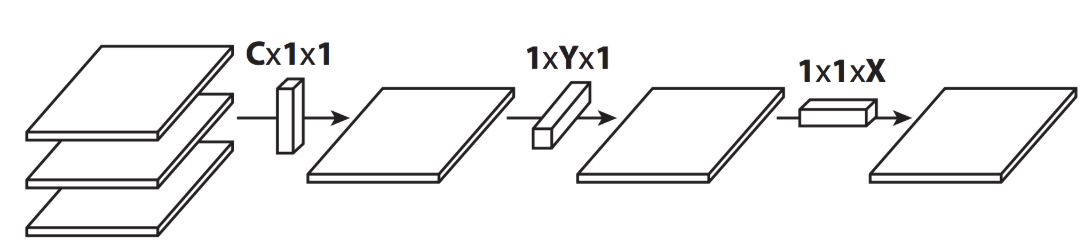

Shuffled Grouped Convolutions

三种类型的卷积组合：

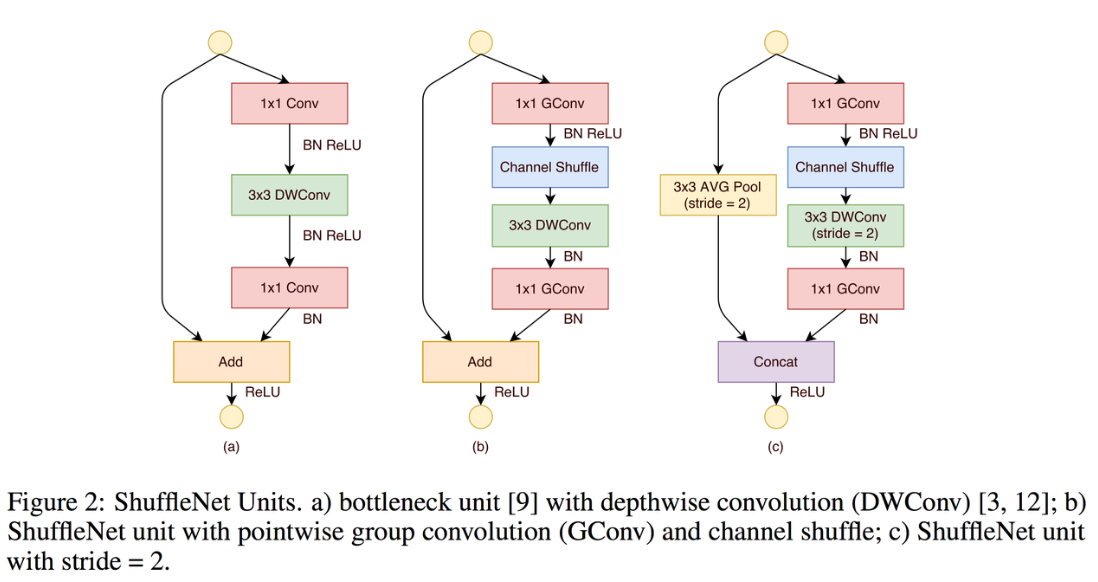
• shuffled grouped convolution = grouped convolution + Channel Shuffle
• pointwise grouped convolution = 1x1 convolution + grouped convolution
• depthwise separable convolution
  Channel Shuffle 操作主要是为了消除原来 Grouped Convolution 中存在的副作用，也就是输出 feature 。 map 的通道仅仅来自输入通道的一小部分，因此每个滤波器组仅限于学习一些特定的特性，如下图所示。
  Grouped Convolution 的这个属性会阻碍信息在通道组之间的信息流动并削弱了模型的表达。通过使用 Channel Shuffle 可以促进通道间信息的融合从而解决以上问题。
  
  

Deformable Convolution

DCN提出的动机是为何特征提取形状一定要是正方形或者矩形，为何不能更加自适应的分布到目标上（如下图右侧所示），进而提出了一种形状可学习的卷积。

Attention

Squeeze and Excitation

SENet的核心想法是，每个通道的重要性不是一样的。基于这个想法，SENet添加了一个模块，如上图靠上的分支，这个模块作用是给每个通道打分，最终将打分的结果与卷积得到的feature map相乘，完成特征通道的权重重分配。SENet是通道注意力机制的最经典的实现。

Convolutional Block Attention Module

CBAM模块算是比较早的一批将通道注意力机制和空间注意力机制结合起来的模型，通过添加该模块，能在一定程度上优化feature。
CBAM 分为 Channel Attention Module 和 Spatial Attention Module

Summary

卷积核的设计非常多，以上仅仅是一部分常见的卷积核，以上卷积核可以这样分类：

• 通道和空间
  Convolution
  1x1 Convolution
  Spatial and Cross-Channel Convolutions
• 通道相关性（channel）
  Depthwise Separable Convolutions
  Shuffled Grouped Convolutions
  Squeeze and Excitation Network
  Channel Attention Module in CBAM
• 空间相关性（HxW）
  Spatially Separable Convolutions
  Flattened Convolutions
  Dilated Convolutions
  Deformable Convolution
  Spatial Attention Module in CBAM

现在很多 CNN 模型准确率越来越高，很多研究人员的研究方向也转向如何在尽可能保证准确率的情况下，尽可能减少模型参数，做好准确率和速度的平衡。
其中ShuffleNet系列效果得到了认可（ShuffleNetV2是腾讯扫一扫项目和ThudnerNet的backbone）。
总结一下效果优异的人工设计的backbone可能会用到以下策略：

1. 单一尺寸卷积核用多个尺寸卷积核代替（参考Inception系列）
2. 使用可变形卷积替代固定尺寸卷积（参考DCN）
3. 大量加入1x1卷积或者 pointwise grouped convolution 来降低计算量（参考NIN、ShuffleNet）
4. 通道加权处理（参考SENet）
5. 用深度可分离卷积替换普通卷积（参考MobileNet）
6. 使用分组卷积（参考ResNeXt）
7. grouped convolution + channel shuffle（参考shuffleNet）
8. 使用 Residual 连接（参考ResNet）

Different types of the convolution layers