Loss 损失函数
熵
考虑另一个问题,对于某个事件,有 n 种可能性,每一种可能性都有一个概率 $p(x_i)$
这样就可以计算出某一种可能性的信息量。举一个例子,假设你拿出了你的电脑,按下开关,会有三种可能性,下表列出了每一种可能的概率及其对应的信息量:
| 序号 | 事件 | 概率 | 信息量 |
|---|---|---|---|
| A | 电脑正常开机 | 0.7 | -log(p(A))=0.36 |
| B | 电脑无法开机 | 0.2 | -log(p(B))=1.61 |
| C | 电脑爆炸了 | 0.1 | -log(p(C))=2.30 |
我们现在有了信息量的定义,而熵用来表示所有信息量的期望,即数学期望相反数:
$$H(X) = -\sum_{i=1}^n p(x_i)log(p(x_i))$$
其中 n 代表所有的 n 种可能性,所以上面的问题结果就是:
$$
H(X)=−[p(A)log(p(A))+p(B)log(p(B))+p(C)log(p(C))]\\
=0.7×0.36+0.2×1.61+0.1×2.30\\
=0.804
$$
如果是掷硬币只有两种可能的问题简化如下公式:
$$
H(X) = -\sum_{i-1}^n p(x_i)log(p(x_i))\\
= - p(x)log(p(x)) - (1-p(x))log(1-p(x))
\ (*)$$
我们将公式 * 称之为 0-1 分布(二项分布)问题。
相对熵
相对熵又称 KL 散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x),我们可以使用 KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异。
Tips:
机器学习领域内:
DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.
即如果用 Q 代替 P 来描述目标问题,得到的“信息增量”(用比值表示增量)。
在机器学习中,P 往往用来表示样本的真实分布,比如 [1,0,0]表示当前样本属于第一类。Q 用来表示模型所预测的分布,比如 [0.7,0.2,0.1]
直观的理解就是如果用 P 来描述样本,那么就非常完美。而用 Q 来描述样本,虽然可以大致描述,但是不是那么的完美,信息量不足,需要额外的一些 “信息增量” 才能达到和 P 一样完美的描述。如果我们的 Q 通过反复训练,也能完美的描述样本,那么就不再需要额外的 “信息增量”,即“信息增量”趋于零,Q 等价于 P。
KL散度的计算公式:
$$
D_{KL}(p||q) = \sum_{i=1}^n p(x_i)log(\frac {p(x_i)}{q(x_i)})
\ (**)
$$
连续事件用积分代替求和
n 为事件的所有可能性或者是所有的样本类别。
$D_{KL}$ 的值越小,表示 q 分布和 p 分布越接近
如果 p q 顺序交换,则需要使用 q 的熵,所以是非对称的
交叉熵(CE)
由 KL 散度公式推导:
$$
D_{KL}(p||q) = \sum{i=1}^n p(x_i)log(p(x_i)) - \sum_{i=1}^n p(x_i)log(q(x_i))
= -H(p(x_i)) + [-\sum_{i=1}^n p(x_i)log(q(x_i))]
$$
等式的前一部分恰巧就是 p 的熵(|数学期望|),等式的后一部分,就是交叉熵:
$H(p,q) = -\sum_{i=1}^n {p_{x_i}logq_{x_i}}$
需要评估 label (p) 和 predicts (q) 之间的差距,使用 KL 散度刚刚好,即 $D_{KL}( y || \hat y)$ ,其中 $y=p(x_i) \hat y = q(x_i)$,得:
$$H(y,\hat y) = -sum_{i=1}^n y log \hat y$$
由于 KL 散度中的前一部分 −H(y)不变,故在优化过程中,只需要关注交叉熵就可以了。所以一般直接用交叉熵做 loss,评估模型。
当 p 与 q 的分布一致时, 交叉熵 $H(p,q)$ 有最小值。
- MSE(Mean Squared Error)
$loss = \frac {1}{2m}\sum_{i=1}^n (y_i - \hat y_i)$
这里的 m 表示 m 个样本的,loss 为 m 个样本的 loss 均值。
MSE 在线性回归问题中比较好用。
交叉熵在单分类问题中的使用
这里的单类别是指,每一张图像真实样本 P 只能有一个类别,比如只能是狗或只能是猫。
交叉熵在单分类问题上基本是标配的方法
$$loss = -sum_{i=1}^n y_i log(\hat y_i)$$
其中,$n$ 表示类别数,$y_i$是一个 one-hot 向量,元素只有 0 和 1 两种取值,如果该类别和样本的类别相同就取 1,否则取 0,$\hat y_i$ 表示预测样本属于 i 的概率。
上式为一张样本图片的 loss 计算方法。
例子:
有一个样本是青蛙
对应的标签和预测值:
| 种类 | 狗 | 青蛙 | 猫 |
|---|---|---|---|
| label | 0 | 1 | 0 |
| pred | 0.3 | 0.6 | 0.1 |
根据交叉熵公式得:
$$
loss=−(0×log(0.3)+1×log(0.6)+0×log(0.1))\\
=−log(0.6)
$$
上面的例子中 label 为一个 one-hot 向量,简化公式:
$$
NLL = -log \hat y_i
$$
对应一个 batch 的 loss 就是:
$$
loss = -\frac {1}{m}\sum_{j=1}^m \sum_{i=1}^n y_{ji}log(\hat y_{ji})
$$
m 为当前 batch 的样本总数
单分类简化公式:
$$
loss = -\frac {1}{m}\sum_{j=1}^m log (y_{j})
$$
交叉熵在多分类问题中的使用
这里的多类别是指,每一张图像样本可以有多个类别,比如同时包含一只猫和一只狗
和单分类问题的标签不同,多分类的标签是n-hot。
当类别数 $n$ 等于 2 的时候,这个损失就是二元交叉熵 Loss,BCE。
例子:
有一个样本是青蛙和猫
对应的标签和预测值:
| 种类 | 狗 | 青蛙 | 猫 |
|---|---|---|---|
| label | 0 | 1 | 1 |
| pred | 0.1 | 0.7 | 0.8 |
注意,因为 n=2 所以这里的 Pred 不再是通过 softmax 计算的了,这里采用的是 sigmoid。将每一个节点的输出归一化到 [0,1] 之间。所有 Pred 值的和也不再为 1。换句话说,就是每一个 Label 都是独立分布的,相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算,每一个节点只有两种可能值,所以是一个二项分布。前面说过对于二项分布这种特殊的分布,熵的计算可以进行简化。
$$
loss = -y log(\hat y) - (1 - y) log(1 - \hat y)
$$
注意,上式只是针对一个类别的计算公式。这一点一定要和单分类 loss 区分开来。
例子中可以计算为:
$$
loss_{狗} = -0 * log(0.1) - (1-0)log(1-0.1) = -log(0.9)
loss_{青蛙} = -1 * log(0.7) - (1-1)log(1-0.7) = -log(0.7)
loss_{鼠} = -1 * log(0.8) - (1-1)log(1-0.8) = -log(0.8)
$$
单张样本的 loss 即为 $loss = loss_{狗} + loss_{青蛙} + loss_{鼠}$
每一个 batch 的 loss 就是:
式中 m 为当前 batch 中的样本量,n 为类别数。
在 Pytorch 中提供了 BCE 一个单独的实现。
Pytorch 实验:
import torch
import torch.nn as nn
import torch.nn.functional as F
# 二元交叉熵,这里输入要经过sigmoid处理
nn.BCELoss(F.sigmoid(input), target)
# 多分类交叉熵, 用这个 loss 前面不需要加 Softmax 层
nn.CrossEntropyLoss(input, target)
"""
nn.NLLLoss
官方文档中介绍称: nn.NLLLoss输入是一个对数概率向量和一个目标标签,它与nn.CrossEntropyLoss的关系可以描述为:
softmax(x)-->log(x)-->nn.NLLLoss====>nn.CrossEntropyLoss
"""
import torch
# (1)
input=torch.randn(3,3)
soft_input = torch.nn.Softmax(dim=0)
soft_input(input)
# Out[20]:
# tensor([[0.7284, 0.7364, 0.3343],
# [0.1565, 0.0365, 0.0408],
# [0.1150, 0.2270, 0.6250]])
# 对 softmax 结果取log, 然后将概率最大的取出来
torch.log(soft_input(input))
Out[21]:
tensor([[-0.3168, -0.3059, -1.0958],
[-1.8546, -3.3093, -3.1995],
[-2.1625, -1.4827, -0.4701]])
(0.3168+3.3093+0.4701)/3
# Out[22]: 1.3654000000000002
# (2)
#验证一下
loss=torch.nn.NLLLoss()
target=torch.tensor([0,1,2])
loss(input,target)
# Out[26]: tensor(0.1365)
# (3)
loss=torch.nn.NLLLoss()
target=torch.tensor([0,1,2])
loss(input,target)
Out[26]: tensor(-0.1399)
loss =torch.nn.CrossEntropyLoss()
input = torch.tensor([[ 1.1879, 1.0780, 0.5312],
[-0.3499, -1.9253, -1.5725],
[-0.6578, -0.0987, 1.1570]])
target = torch.tensor([0,1,2])
loss(input,target)
# Out[30]: tensor(0.1365)
交叉熵 Loss 可以用在大多数语义分割场景中,但它有一个明显的缺点,那就是对于只用分割前景和背景的时候,前景像素的数量远远小于背景像素的数量时,即的数量远大于的数量,损失函数中的成分就会占据主导,使得模型严重偏向背景,导致效果不好。
带权交叉熵 Loss
带权重的交叉熵Loss,公式为:$L = -\sum_{c=1}^M w_c y_c log(p_c)$
可以看到只是在交叉熵 Loss 的基础上为每一个类别添加了一个权重参数,其中 $w_c$ 的计算公式为:
$$w_c = \frac {N-N_c}{N}$$
其中 N 表示总的像素个数,而 $N_c$ 表示 GT 类别为 c 的像素个数。这样相比于原始的交叉熵 Loss,在样本数量不均衡的情况下可以获得更好的效果。
Negative log loss (NLL)
$L_{i} = -\log(\frac{e^{y_{i}}}{\sum_{j}e^{y_j}})$
NNL 是 CE 的一种应用形式,使用的就是 CE 的计算公式,但在通常看到的计算形式是这种: $-log\hat y_i$ .
首先 CE 计算的是两个分布(真实分布与预测分布)之间的交叉熵,即距离,以此距离值作为损失值。而在多分类(multi-class)任务中,预测分布式模型经过 softmax 函数后的输出 vector,而真实分布则是每个输出目标类(ground truth)的 onehot 编码,将该值带入 CE 公式后就得到上面的公式。
Focal Loss
RetinaNet 论文中引入了 Focal Loss 来解决难易样本数量不平衡,One-Stage 的目标检测器通常会产生 10k 数量级的框,但只有极少数是正样本,正负样本数量非常不平衡。我们在计算分类的时候常用的损失——交叉熵的公式如下:
$$CE(p,y) =
\begin{cases}
-log(p),&if\ y = 1 \\
-log(1-p),&otherwise \\
\end{cases}
\ (1)$$
p 表示样本属于 true class 的概率,有时也用 $p_t$ 表示。
为了解决正负样本数量不平衡的问题,我们经常在二元交叉熵损失前面加一个参数 $\alpha$,即:
$$BCE =
\begin{cases}
-\alpha log(p),&if\ y = 1 \\
-(1-\alpha)log(1-p),&if\ y = 0 \\
\end{cases}
\ (2)$$
虽然 $\alpha$ 平衡了正负样本的数量,但实际上,目标检测中大量的候选目标都是易分样本。这些样本的损失很低,但是由于数量极不平衡,易分样本的数量相对来讲太多,最终主导了总的损失。
易分样本(即,置信度高的样本)对模型的提升效果非常小,模型应该主要关注与那些难分样本 。所以 Focal Loss 横空出世了。一个简单的想法就是只要我们将高置信度样本的损失降低一些就好了吧? 也即是下面的公式:
$$FL =
\begin{cases}
-(1-p)^{\gamma} log(p),&if\ y = 1 \\
-p^{\gamma} log(1-p),&if\ y = 0 \\
\end{cases}
\ (3)$$
p 表示样本属于 true class 的概率,这里的 γ 称作 focusing parameter,γ >= 0,$(1-p)^{\gamma}$ 称为调制因子(modulating factor)。
为什么要加上这个调制系数呢?目的是通过减少易分类样本的权重,从而使得模型在训练时更专注于难分类的样本。
我们取等于 2 来感受一下,如果 $p=0.9$,那么 $(1-0.9)^2 = 0.001$,损失降低了 1000 倍。最终 Focal Loss 还结合了公式 (2),这很好理解,公式 (3) 解决了难易样本的不平衡,公式 (2) 解决了正负样本的不平衡,将公式(2)与(3)结合使用,同时解决正负难易 2 个问题!所以最终 Focal Loss 的形式如下:
$$FL =
\begin{cases}
-\alpha(1-p)^{\gamma} log(p),&if\ y = 1 \\
-(1-\alpha)p^{\gamma} log(1-p),&if\ y = 0 \\
\end{cases}
\ (3)$$
下面这张图展示了 Focal Loss 取不同的 $\gamma , \alpha$ 时的损失函数下降。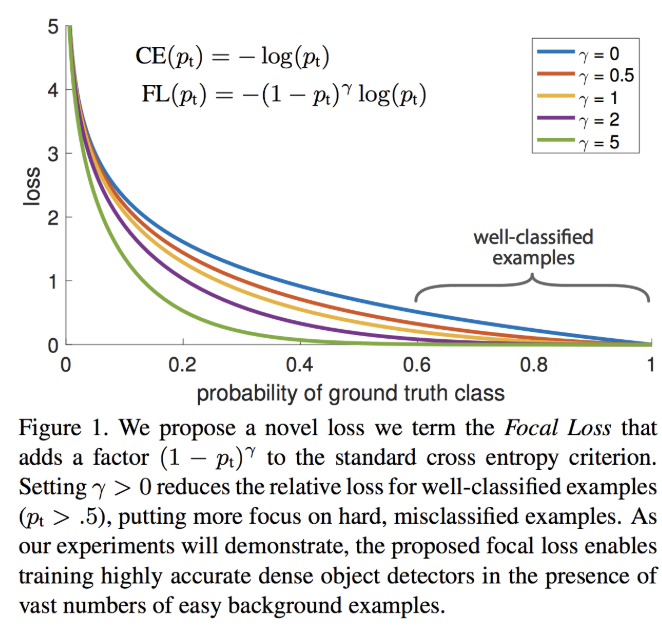
Figure1 横坐标是 $p_t$,纵坐标是 loss。$CE(p_t)$ 表示标准的交叉熵公式,$FL(p_t)$ 表示 Focal Loss 中用到的改进的交叉熵。其中 γ=0 的蓝色曲线就是标准的交叉熵损失。
实验结果展示,当 $\gamma = 2,\alpha = 0.75$ 时,效果最好,这样损失函数训练的过程中关注的样本优先级就是:
正难 > 负难 > 正易 > 负易。
虽然在 RetinaNet 中取是最好的,但是不代表这个参数在我们的分割任务和其他样本上是最好的,我们需要手动调整这个参数,另外 Focal Loss 在分割任务上似乎是只适合于二分类的情况。
这里介绍下 Focal Loss 的两个重要性质:
- 当一个样本被分错的时候,p 是很小的,那么调制因子 1-p 接近1,损失不被影响;当 p → 1,因子 1-p 接近 0,那么分的比较好的(well-classified)样本的权值就被调低了。因此调制系数就趋于 1,也就是说相比原来的 loss 是没有什么大的改变的。当 p 趋于 1 的时候(此时分类正确而且是易分类样本),调制系数趋于 0,也就是对于总的 loss 的贡献很小。
当 γ=0 的时候,Focal Loss 就是传统的交叉熵损失,当 γ 增加的时候,调制系数也会增加。 专注参数 γ 平滑地调节了易分样本调低权值的比例。 γ 增大能增强调制因子的影响,实验发现 γ 取 2 最好。直觉上来说,调制因子减少了易分样本的损失贡献,拓宽了样例接收到低损失的范围。当 γ 一定的时候,比如等于 2,一样 easy example(p=0.9) 的 loss 要比标准的交叉熵 loss 小 100+ 倍,当 p=0.968 时,要小 1000+ 倍,但是对于 hard example(p < 0.5),loss 最多小了 4 倍。这样的话 hard example 的权重相对就提升了很多。这样就增加了那些误分类的重要性。
这两个性质算是核心,其实就是用一个合适的函数去度量难分类和易分类样本对总的损失的贡献。class FocalLoss(nn.Module): def __init__(self, gamma=0, alpha=None, size_average=True): super(FocalLoss, self).__init__() self.gamma = gamma self.alpha = alpha if isinstance(alpha,(float,int,long)): self.alpha = torch.Tensor([alpha,1-alpha]) if isinstance(alpha,list): self.alpha = torch.Tensor(alpha) self.size_average = size_average def forward(self, input, target): if input.dim()>2: input = input.view(input.size(0),input.size(1),-1) # N,C,H,W => N,C,H*W input = input.transpose(1,2) # N,C,H*W => N,H*W,C input = input.contiguous().view(-1,input.size(2)) # N,H*W,C => N*H*W,C target = target.view(-1,1) logpt = F.log_softmax(input) logpt = logpt.gather(1,target) logpt = logpt.view(-1) pt = Variable(logpt.data.exp()) if self.alpha is not None: if self.alpha.type()!=input.data.type(): self.alpha = self.alpha.type_as(input.data) at = self.alpha.gather(0,target.data.view(-1)) logpt = logpt * Variable(at) loss = -1 * (1-pt)**self.gamma * logpt if self.size_average: return loss.mean() else: return loss.sum()
Dice Loss
在很多关于医学图像分割的竞赛、论文和项目中,发现 Dice 系数(Dice coefficient) 损失函数出现的频率较多,关于分割中 Dice Loss 和交叉熵损失函数(cross-entropy loss)
Dice系数, 根据 Lee Raymond Dice[1] 命名,是一种集合相似度度量函数,通常用于计算两个样本的相似度(值范围为 [0, 1]):
$$s = \frac {2|X\bigcap Y|}{|X|+|Y|}$$
相对比 IOU 上下都多了一个 $\bigcap$
$|X\bigcap Y|$ 是 X 和 Y 之间的交集,|X| 和 |Y| 分别表示 X 和 Y 的元素个数,其中,分子中的系数 2,是因为分母中存在重复计算 X 和 Y 之间的共同元素。
语义分割问题:
X : GT 分割图像, Y : Pred 分割图像
Dice 系数差异函数(Dice loss):
$$d = 1 - \frac {2|X\bigcap Y|}{|X|+|Y|}$$
拉普拉斯平滑 分子分母都加 1 ,防止 |X|、|Y| 出现等于 0 的情况。
计算示例:
预测的分割图的 dice 系数计算,首先将 $|X\bigcap Y|$ 近似为预测图与 GT 分割图之间的点乘,并将点乘的元素结果相加。
Tversky Loss
Exponential Logarithmic loss
Lovasz-Softmax Loss
loss 组合
- BCE + Dice Loss
即将BCE Loss和Dice Loss进行组合,在数据较为均衡的情况下有所改善,但是在数据极度不均衡的情况下交叉熵Loss会在迭代几个Epoch之后远远小于Dice Loss,这个组合Loss会退化为Dice Loss。 - Focal Loss + Dice Loss
Focal Loss for Dense Object Detection (Paper Summary)
为什么交叉熵(cross-entropy)可以用于计算代价?
Kullback–Leibler divergence
Why You Should Use Cross-Entropy Error Instead Of Classification Error Or Mean Squared Error For Neural Network Classifier Training
医学图像分割之 Dice Loss
请多多指教。
文章标题:Loss 损失函数
本文作者:顺强
发布时间:2019-03-05, 23:59:00
原始链接:http://shunqiang.ml/cnn-loss-function/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

