图

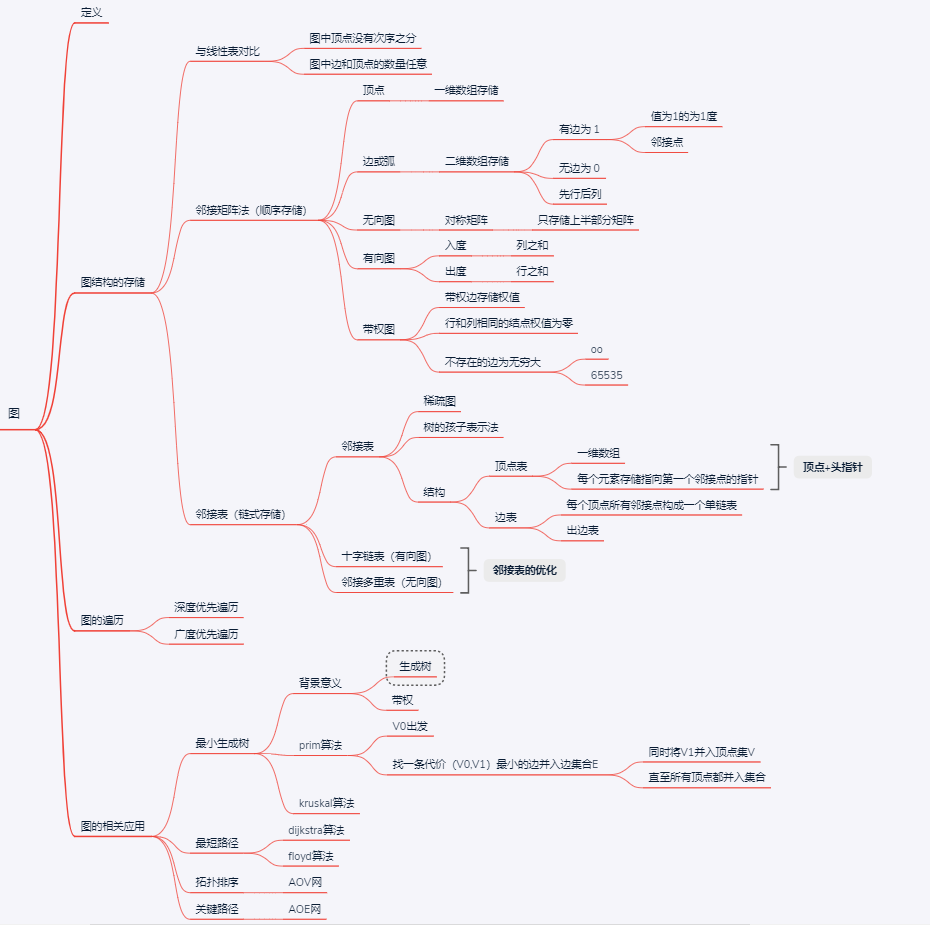
基本概念

图分为有向图和无向图。
图 G 由顶点集 V 和边集 E 组成，记为 G=(V，E)。 V(G) 表示图 G 中顶点的有限非空集。
用 |V| 表示图 G 中顶点的个数，也称为图 G 的阶。E(G) 表示图 G 中顶点之间的关系（边）集合。用 |E| 表示图 G 中边的条数。
图不可为空，一个图中就算是一条边都没有，也就是边集为空，但是顶点集一定不为空。

完全图：任意两个顶点之间都存在边。
子图
连通图：图中任意两个顶点都是连通的

图的存储结构

邻接矩阵（顺序存储）
顶点：用一维数组来存储, 边或弧：用二维数组来存储
二维数组就是一维数组的拓展，相当于一维数组中每个元素也是一个一维数组。二维数组也叫做邻接矩阵
无向图的邻接矩阵是一个对称矩阵

邻接表（链式存储）
对于稀疏图(|E| 远小于 $|V|^2$) 顺序存储结构存在预先分配内存可能浪费的问题，按照经验会想到链式存储结构
图中的顶点用一个一维数组存储。同时每个元素还要存储指向第一个邻接点的指针(链表的头指针)。存储顶点和头指针的表叫顶点表。
图中每个顶点的所有邻接点构成一个单链表。对于无向图，这个表称为该结点的边表，对于有向图称为该结点的出边表。

十字链表
有向图的邻接表关心了有向图的出边问题，我们通过有向图很容易找到顶点的出边。
比如从每个顶点表的 firstedge 指针找到第一条边的顶点，再通过 next 指针依次找到下一条边的顶点直到空指针。
但是，如果要找到其他顶点到该顶点的边，或者说考虑一个顶点的入度问题，则需要遍历整个图。这是邻接表存储有向图的缺陷。
十字链表是针对有向图的存储方式，对应于有向图中的每条弧有一个结点，对应于每个顶点也有一个结点。
其实十字链表是在邻接表的基础上进行了优化。在十字链表中不仅包含了邻接表本身就包含的结点出度结点，而且还包含了入度结点的信息。

邻接多重表
邻接表存储的无向图中查找顶点是比较容易的，但是如果要修改图中的边或者是查询边,则需要遍历链表。这是邻接表的缺陷。
仿照十字链表，对邻接表的边表进行改造，得到专门针对存储无向图的邻接多重表。

图的遍历

从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这个过程就叫做图的遍历。
深度优先遍历
深度优先搜索(DFS:Depth-First-Search):深度优先搜索类似于树的先序遍历算法。
首先访问图中某一起始顶点v，然后由v出发，访问与v邻接且未被访问的任一顶点w1，再访问与w1邻接且未被访问的任一顶点w2，……重复上述过程。当不能再继续向下访问时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直到图中所有顶点均被访问过为止
空间复杂度：由于DFS是一个递归算法，递归是需要一个工作栈来辅助工作，最多需要图中所有顶点进栈，所以时间复杂度为O(|V|)
时间复杂度：
1)邻接表：遍历过程的主要操作是对顶点遍历它的邻接点，由于通过访问边表来查找邻接点，所以时间复杂度为 O(|E|),访问顶点时间为 O(|V|),所以总的时间复杂度为 O(|V|+|E|)
2)邻接矩阵：查找每个顶点的邻接点时间复杂度为 O(|V|),对每个顶点都进行查找，所以总的时间复杂度为 O(|V|2)。

广度优先遍历
广度优先搜索(BFS:Breadth-First-Search):广度优先搜索类似于树的层序遍历算法。
BFS解决单源非带权图最短路径问题：按照距离由近到远来遍历图中每个顶点

最小生成树

之前讲过连通图的生成树，它是一个极小的连通子图。它包含图中全部的顶点，但只有足以构成一棵树的n-1条边。生成树不唯一。
选择总权值最小的修路成本自然最小
普利姆(Prim)算法:
①从图中找第一个起始顶点v0，作为生成树的第一个顶点，然后从这个顶点到其他顶点的所有边中选一条权值最小的边。然后把这条边的另一个顶点v和这条边加入到生成树中。
②对剩下的其他所有顶点，分别检查这些顶点与顶点v的权值是否比这些顶点在lowcost数组中对应的权值小，如果更小，则用较小的权值更新lowcost数组。
③从更新后的lowcost数组中继续挑选权值最小而且不在生成树中的边，然后加入到生成树。
④反复执行②③直到所有所有顶点都加入到生成树中。