53. Maximum Subarray

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:
If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

实际场景

在实际生活中，通常会出现一个场景，炒股的人盯着一只股票涨跌情况在分析这只股票一段时间内，何时买进买出才能达到收益的最大化。通常人们想到的是“低价买进，高价卖出”，这是最理想的情况，但是实际情况中，你可能无法做到。比如下图中股票 A，最高价格出现在第 0 天，而最低价格出现在第 3 天，显然无法做到低买高卖。于是你可能会想也许满足其中的任意一个条件，得到的结果就是最优结果。不否认，股票 A 如果在第 3 天最低价的时候买进，确实能达到收益最大化。但是股票 B 给出了一个反例，最大收益既不是在最低价格时买进，也不是在最高价格时卖出。

分治策略求解

分治策略，最常见的实际应用就是归并排序。说到分治策略，就是递归地求解一个问题。在每层递归中分三个步骤解决问题：

• 分解（Devide），将问题划分为相同的子问题；
• 解决（Conquer），求解子问题，如果达到条件直接求解，未达到条件则继续递归；
• 合并（Combine），将子问题的解合成原问题的解。
  递归的计算方式有通用公式：T(n) = aT(n/b) + f(n)。
  最大子数组每次都是最数组进行二等分，所以公式为：T(n) = 2T(n/2) + f(n)，那么时间复杂度就是 O(nlgn)。
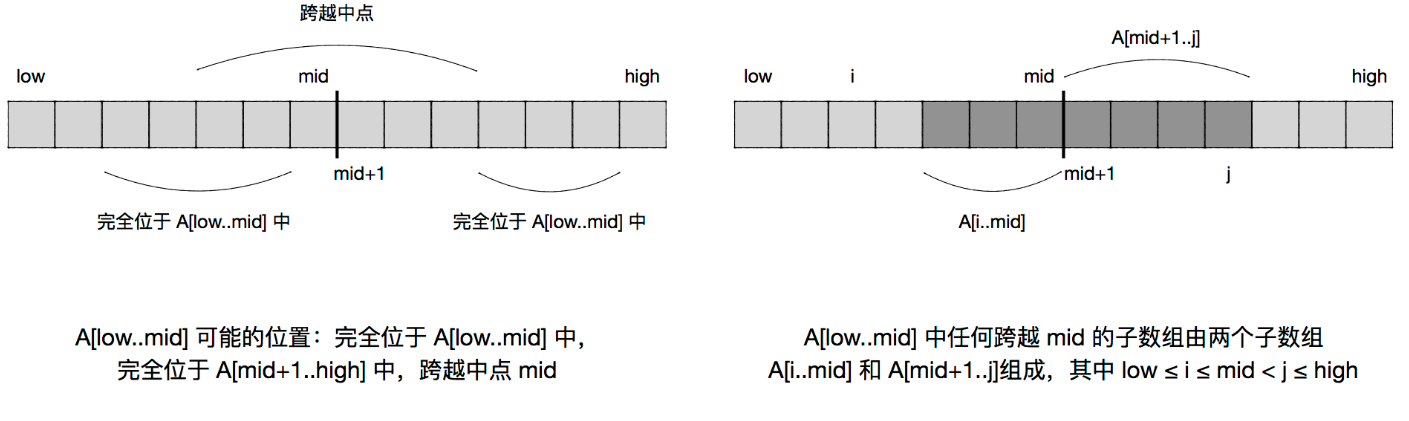
  我们要通过分治策略来寻找数组 A[low..high] 的最大子数组，意味着我们要将子数组划分为两个规模相等的子数组。首先找到子数组的中央位置 mid，然后考虑求解两个子数组 A[low..mid] 和 A[mid+1..high]。我们很容易发现最大子数组 A[i..j] 所处的位置必然是以下情况之一：
• 完全位于子数组 A[low..mid] 中，那么 low ≤ i ≤ j ≤ mid
• 完全位于子数组 A[mid+1..high] 中，那么 mid < i ≤ j ≤ high
• 子数组跨越了中点，那么 low ≤ i ≤ mid < j ≤ high
  

class Solution(object):
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        return self.maxSubSum(nums, 0, len(nums) - 1)

    def maxSubSum(self, subArray, left, right):
        if left == right :
            return subArray[left]

        mid = (left + right) // 2
        maxLeftSum = -sys.maxsize - 1
        maxRightSum = -sys.maxsize - 1
        maxMidSum = -sys.maxsize - 1
        maxLeftSum = self.maxSubSum(subArray, left, mid)
        maxRightSum = self.maxSubSum(subArray, mid + 1, right)
        maxMidSum = self.maxCrossingSubSum(subArray, left, mid, right)
        return max(maxLeftSum, maxRightSum, maxMidSum)

    def maxCrossingSubSum(self, subArray, left, mid, right):
        sum = 0
        maxLeftSum = -sys.maxsize - 1
        maxRightSum = -sys.maxsize - 1
        for i in range(mid,left-1,-1) :
            sum += subArray[i]
            maxLeftSum = max(sum, maxLeftSum)
        sum = 0
        for i in range(mid+1, right+1) :
            sum += subArray[i]
            maxRightSum = max(sum, maxRightSum)
        return maxLeftSum + maxRightSum

动态规划求解

动态规划（dynamic programming）与分治策略相似，这里的 programming 指的是一种表格法，都是通过组合子问题的解来求解原问题。分治法将问题划分为互不相交的子问题，递归的求解子问题，再将他们的解组合起来，求出原问题的解。与之相反，动态规划应用于 子问题重叠 的情况，即不同的子问题具有公共的子子问题。在这种情况下，分治策略会做许多不必要的工作，它会反复的求解那些公共子子问题。而动态规划算法对每个子子问题只求解一次，将其解保存在一个表格中，从而无需每次求解一个子子问题时都重新计算，避免了这种不必要的工作。

动态规划方法通常用来求解 最优化问题，这类问题可以有很多可行解，每个解都有一个值，我们希望寻找具有最优值（最小值或最大值）的解。我们称这样的解为问题的一个最优解，而不是最优解，因为可能有多个解都达到最优值。

通常按照 4 个步骤来设计动态规划算法：

• 寻找一个最优解的结构特征。
• 递归的定义最优解的值。
• 计算最优解的值，通常采用自底向上的方法。
• 利用计算出的信息构造一个最优解。

最大子数组里面，我们首先要想清楚一个问题就是对于 maxSubArray(A, i) 来说，如果它是目前最大的数组，那么子数组 maxSubArray(A, i - 1) 一定是非负数，因为 maxSubArray(A, i - 1) > maxSubArray(A, i - 1) + A[i]，所以不难得出一个结论：maxSubArray(A, i) = maxSubArray(A, i - 1) > 0 ? maxSubArray(A, i - 1) + A[i] : A[i];

class Solution(object):
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        sum = 0
        # state
        maxSum = - sys.maxsize - 1
        for num in nums :
            sum = max(num, sum + num)
            maxSum = max(maxSum, sum)
        return maxSum

1. leetcode record