词向量

onehot 向量不能表示词与词之间的关系

word2vec 工具
模型: skip-gram 和 CBOW
训练方法：负采样和层序 softmax

skip-gram 算法思想
我 爱 北京 天安门 –> vocab dict [. . . . ]

Num_skips = 2 表示input用了产生label的次数限制
assert batch_size % num_skips == 0
assert num_skips <= 2 * skip_window

以句子The quick brown fox jumps over the lazy dog为例，实现过程为
1. 选定词语fox作为input-word
2. 定义skip-window作为input-word的上下文范围，如skip-window=2，fox的上下文为quick，brown, jumps, over 。
组成的样本对(fox,quick),(fox,brown), (fox,jumps), (fox,over)。定义窗口中选取的样本对个数num-skips，如果num-skips=2，skip-window=2，则从四组样本中随机选取两组作为样本。

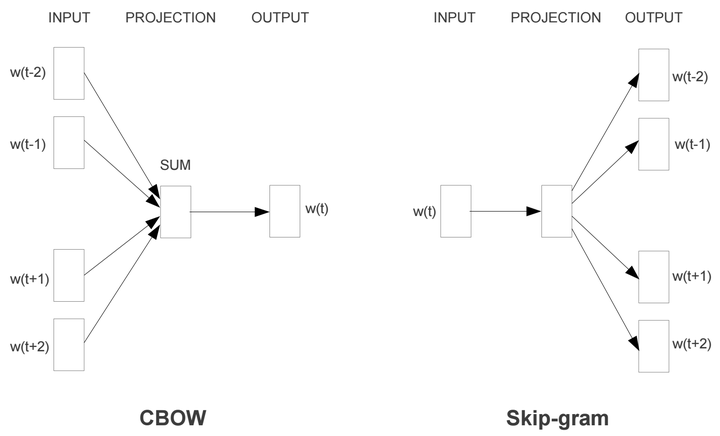
我们先来分析一下skip-gram的样本格式。skip-gram不同于CBOW，CBOW是基于上下文预测当前input word。而skip-gram则是基于一个input word来预测上下文，因此一个input word会对应多个上下文。我们来举个栗子“[熟练掌握 java 熟悉 python shell 熟练使用 git svn]”，如果我们固定skip_window=2的话，那么熟悉的上下文就是[熟练掌握, java, python, shell]，如果我们的batch_size=1的话，那么实际上一个batch中有四个训练样本。

上面的分析转换为代码就是两个步骤，第一个是找到每个input word的上下文，第二个就是基于上下文构建batch。

首先是找到input word的上下文单词列表：

Skip-Gram模型是通过输入词来预测上下文。因此我们要构造我们的训练样本。

对于一个给定词，离它越近的词可能与它越相关，离它越远的词越不相关，这里我们设置窗口大小为5，对于每个训练单词，我们还会在[1:5]之间随机生成一个整数R，用R作为我们最终选择output word的窗口大小。这里之所以多加了一步随机数的窗口重新选择步骤，是为了能够让模型更聚焦于当前input word的邻近词。

跳字模型

跳字模型假设基于某个词来生成它在文本序列周围的词。

在跳字模型中，每个词被表示成两个$d$维向量，用来计算条件概率。假设这个词在词典中索引为$i$，当它为中心词时向量表示为$\boldsymbol{v}_i\in\mathbb{R}^d$，而为背景词时向量表示为$\boldsymbol{u}_i\in\mathbb{R}^d$。设中心词$w_c$在词典中索引为$c$，背景词$w_o$在词典中索引为$o$，给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到：

$$P(w_o \mid w_c) = \frac{\text{exp}(\boldsymbol{u}_o^\top \boldsymbol{v}_c)}{ \sum_{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)},$$

其中词典索引集$\mathcal{V} = {0, 1, \ldots, |\mathcal{V}|-1}$。假设给定一个长度为$T$的文本序列，设时间步$t$的词为$w^{(t)}$。假设给定中心词的情况下背景词的生成相互独立，当背景窗口大小为$m$时，跳字模型的似然函数即给定任一中心词生成所有背景词的概率

$$ \prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} P(w^{(t+j)} \mid w^{(t)}),$$

这里小于1和大于$T$的时间步可以忽略。

训练跳字模型

跳字模型的参数是每个词所对应的中心词向量和背景词向量。训练中我们通过最大化似然函数来学习模型参数，即最大似然估计。这等价于最小化以下损失函数：

$$ - \sum_{t=1}^{T} \sum_{-m \leq j \leq m,\ j \neq 0} \text{log}\, P(w^{(t+j)} \mid w^{(t)}).$$

如果使用随机梯度下降，那么在每一次迭代里我们随机采样一个较短的子序列来计算有关该子序列的损失，然后计算梯度来更新模型参数。梯度计算的关键是条件概率的对数有关中心词向量和背景词向量的梯度。根据定义，首先看到

$$\log P(w_o \mid w_c) =
\boldsymbol{u}_o^\top \boldsymbol{v}_c - \log\left(\sum_{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)\right)$$

通过微分，我们可以得到上式中$\boldsymbol{v}_c$的梯度

$$
\begin{aligned}
\frac{\partial \text{log}\, P(w_o \mid w_c)}{\partial \boldsymbol{v}_c}
&= \boldsymbol{u}_o - \frac{\sum_{j \in \mathcal{V}} \exp(\boldsymbol{u}_j^\top \boldsymbol{v}_c)\boldsymbol{u}_j}{\sum_{i \in \mathcal{V}} \exp(\boldsymbol{u}_i^\top \boldsymbol{v}_c)}\
&= \boldsymbol{u}_o - \sum_{j \in \mathcal{V}} \left(\frac{\text{exp}(\boldsymbol{u}_j^\top \boldsymbol{v}_c)}{ \sum_{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)}\right) \boldsymbol{u}_j\
&= \boldsymbol{u}_o - \sum_{j \in \mathcal{V}} P(w_j \mid w_c) \boldsymbol{u}_j.
\end{aligned}
$$

它的计算需要词典中所有词以$w_c$为中心词的条件概率。有关其他词向量的梯度同理可得。

训练结束后，对于词典中的任一索引为$i$的词，我们均得到该词作为中心词和背景词的两组词向量$\boldsymbol{v}_i$和$\boldsymbol{u}_i$。在自然语言处理应用中，一般使用跳字模型的中心词向量作为词的表征向量。

连续词袋模型

连续词袋模型与跳字模型类似。与跳字模型最大的不同在于，连续词袋模型假设基于某中心词在文本序列前后的背景词来生成该中心词。

因为连续词袋模型的背景词有多个，我们将这些背景词向量取平均，然后使用和跳字模型一样的方法来计算条件概率。设$\boldsymbol{v_i}\in\mathbb{R}^d$和$\boldsymbol{u_i}\in\mathbb{R}^d$分别表示词典中索引为$i$的词作为背景词和中心词的向量（注意符号的含义与跳字模型中的相反）。设中心词$wc$在词典中索引为$c$，背景词$w\{o_1}, \ldots, w_{o_{2m}}$在词典中索引为$o_1, \ldots, o_{2m}$，那么给定背景词生成中心词的条件概率

$$P(w_c \mid w_{o_1}, \ldots, w_{o_{2m}}) = \frac{\text{exp}\left(\frac{1}{2m}\boldsymbol{u}_c^\top (\boldsymbol{v}_{o_1} + \ldots + \boldsymbol{v}_{o_{2m}}) \right)}{ \sum_{i \in \mathcal{V}} \text{exp}\left(\frac{1}{2m}\boldsymbol{u}_i^\top (\boldsymbol{v}_{o_1} + \ldots + \boldsymbol{v}_{o_{2m}}) \right)}.$$

为了让符号更加简单，我们记$\mathcal{W}_o= {w_{o_1}, \ldots, w_{o_{2m}}}$，且$\bar{\boldsymbol{v}}_o = \left(\boldsymbol{v}_{o_1} + \ldots + \boldsymbol{v}_{o_{2m}} \right)/(2m)$，那么上式可以简写成

$$P(w_c \mid \mathcal{W}_o) = \frac{\exp\left(\boldsymbol{u}_c^\top \bar{\boldsymbol{v}}_o\right)}{\sum_{i \in \mathcal{V}} \exp\left(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o\right)}.$$

给定一个长度为$T$的文本序列，设时间步$t$的词为$w^{(t)}$，背景窗口大小为$m$。连续词袋模型的似然函数是由背景词生成任一中心词的概率

$$ \prod_{t=1}^{T} P(w^{(t)} \mid w^{(t-m)}, \ldots, w^{(t-1)}, w^{(t+1)}, \ldots, w^{(t+m)}).$$

训练连续词袋模型

训练连续词袋模型同训练跳字模型基本一致。连续词袋模型的最大似然估计等价于最小化损失函数

$$ -\sum_{t=1}^T \text{log}\, P(w^{(t)} \mid w^{(t-m)}, \ldots, w^{(t-1)}, w^{(t+1)}, \ldots, w^{(t+m)}).$$

注意到

$$\log\,P(w_c \mid \mathcal{W}_o) = \boldsymbol{u}_c^\top \bar{\boldsymbol{v}}_o - \log\,\left(\sum_{i \in \mathcal{V}} \exp\left(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o\right)\right).$$

通过微分，我们可以计算出上式中条件概率的对数有关任一背景词向量$\boldsymbol{v}_{o_i}$（$i = 1, \ldots, 2m$）的梯度

$$\frac{\partial \log\, P(w_c \mid \mathcal{W}_o)}{\partial \boldsymbol{v}_{o_i}} = \frac{1}{2m} \left(\boldsymbol{u}_c - \sum_{j \in \mathcal{V}} \frac{\exp(\boldsymbol{u}_j^\top \bar{\boldsymbol{v}}_o)\boldsymbol{u}_j}{ \sum_{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o)} \right) = \frac{1}{2m}\left(\boldsymbol{u}_c - \sum_{j \in \mathcal{V}} P(w_j \mid \mathcal{W}_o) \boldsymbol{u}_j \right).$$

有关其他词向量的梯度同理可得。同跳字模型不一样的一点在于，我们一般使用连续词袋模型的背景词向量作为词的表征向量。

词向量降维表征方式

词向量计算优化方法：

快速排序分治法的思想，复杂度 $log n$

哈夫曼树（Hunffman Tree）:最优二叉树

文本 车胎/噪音/比较/大
词频 2 5 7 13 权重
编码 110 111 10 0

权重高的放到离根节点近的地方

哈夫曼树的特点：v 个叶子节点，v-1 个中间节点

二分类问题：逻辑回归 （Logistic Regression）sigmoid

graph TB;
    A((root))-->B((大,0))
    A((root))-->C((C,1))
    C((C,1))-->D((比较,0))
    C((C,1))-->E((E,1))
    E((E,1))-->F((车胎,0))
    E((E,1))-->G((噪音,1))

哈夫曼编码：

Genism 代码实践

---

请多多指教。